- 9 oefentoetsen met 120+ oefenvragen
- Binnen 2 minuten starten
Matrixen oefenen
Ga vandaag nog voor matrixen oefenen. Dit oefenpakket bevat lessen en oefeningen voor alle soorten matrixen die je op het matrix assessment kunt krijgen.
Geschikt voor alle soorten matrixen, o.a.:
Wat je ontvangt in de cursus
- 30 dagen toegang
- 120+ oefenvragen met uitleg en antwoorden
- 3 lessen waarin alles wordt uitgelegd
- 9 oefentesten om vragen te maken
- English translations included (see below)
- Voorzien van video uitleg
14,99

Ook te koop als onderdeel van ons totaalpakket.
96% van onze klanten beveelt ons aan!
2.000+ oefenvragen
2.600+ oefenvragen
1.600+ oefenvragen
2.500+ oefenvragen
Matrixen oefenen gratis
Matrixen variatie 1
In deze gratis abstracte matrix test moet je matrixen oplossen.
0 van 5 vragen voltooid Vragen: Je hebt deze test al eerder afgerond, daarom kan je hem niet nog een keer doen.
Quiz is aan het laden… Je moet inloggen om deze quiz te starten. U moet eerst het volgende invullen:
0 van 5vragen goed beantwoord
Jouw tijd:
De tijd is verstreken
Je hebt 0 van 0 punten bereikt, 0
Earned Point(s): 0 of 0, (0)
Quiz samenvatting
Informatie
Resultaten
Resultaten
0 Audio(s)/Essay(s) Pending (Possible Point(s): 0)
Gemiddelde score
Your score
Categorieën
1. Vraag
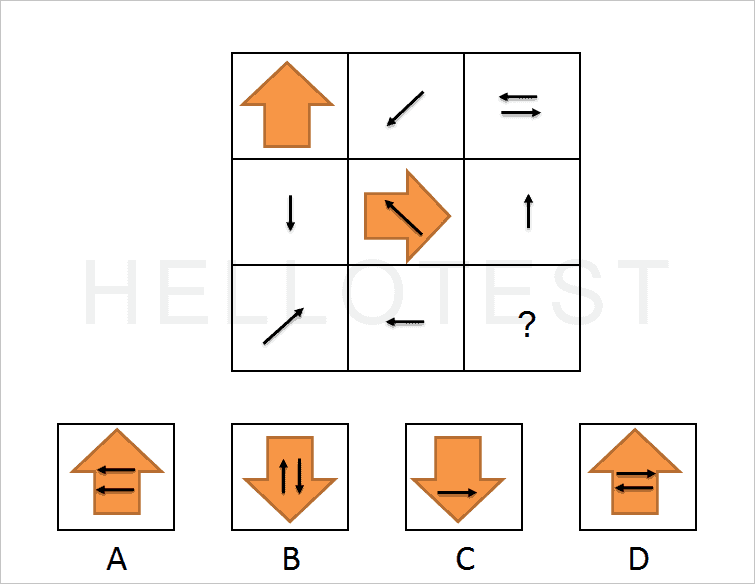
2. Vraag
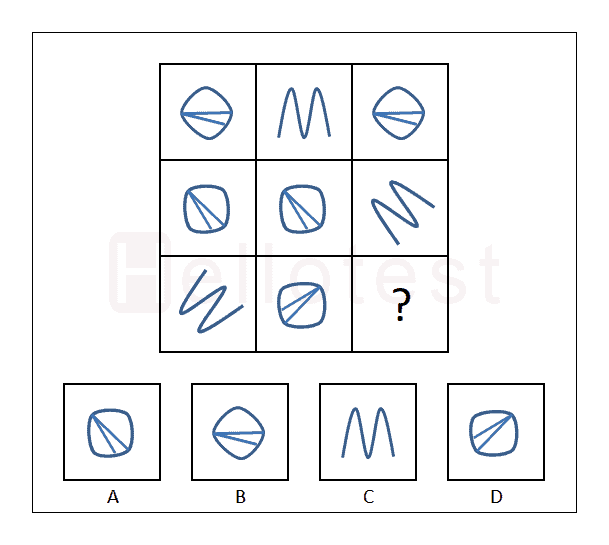
3. Vraag
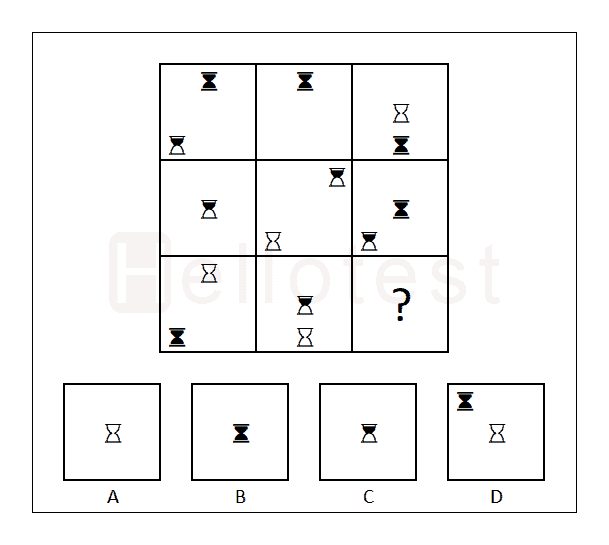
4. Vraag
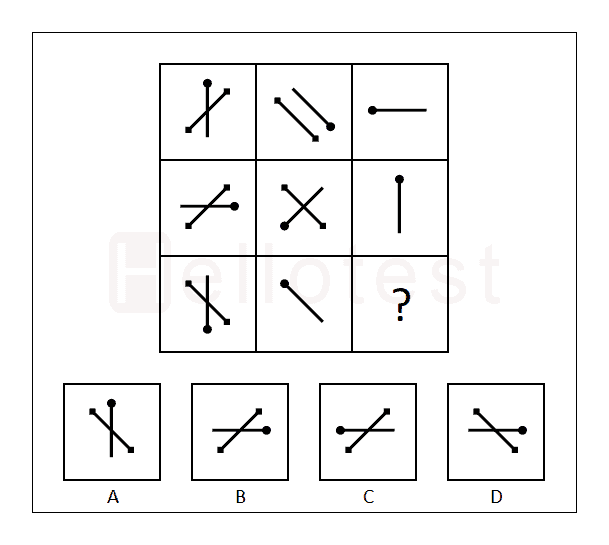
5. Vraag
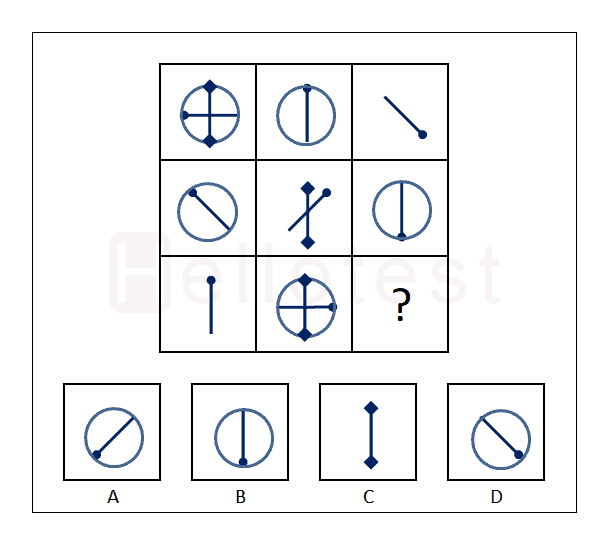
Matrixen variatie 2
In deze abstracte matrix test kan je matrixen gratis oefenen.
0 van 5 vragen voltooid Vragen: Je hebt deze test al eerder afgerond, daarom kan je hem niet nog een keer doen.
Quiz is aan het laden… Je moet inloggen om deze quiz te starten. U moet eerst het volgende invullen:
0 van 5vragen goed beantwoord
Jouw tijd:
De tijd is verstreken
Je hebt 0 van 0 punten bereikt, 0
Earned Point(s): 0 of 0, (0)
Quiz samenvatting
Informatie
Resultaten
Resultaten
0 Audio(s)/Essay(s) Pending (Possible Point(s): 0)
Gemiddelde score
Your score
Categorieën
1. Vraag
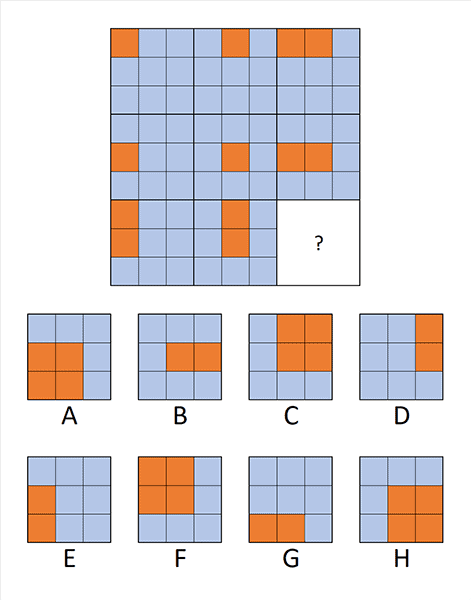
2. Vraag
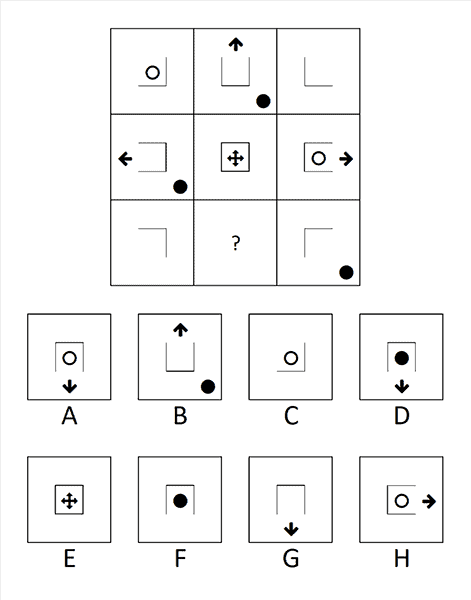
3. Vraag
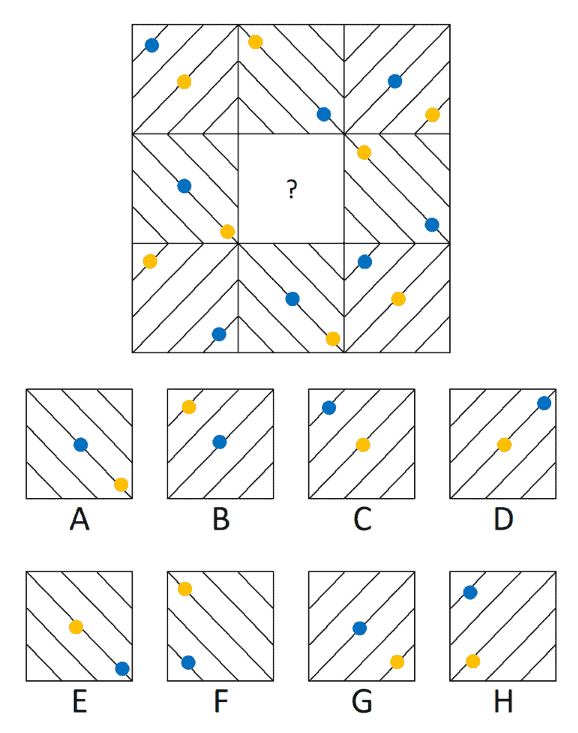
4. Vraag
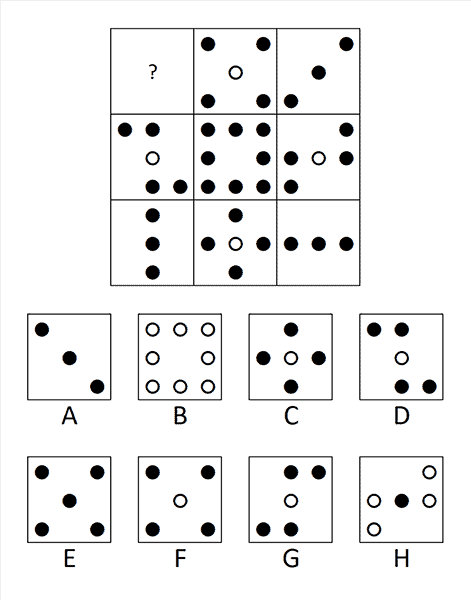
5. Vraag
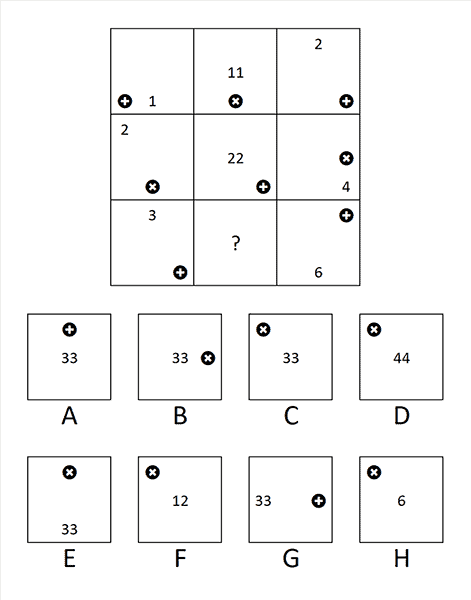
Matrixen variatie 3
In deze abstracte matrix test kan je matrixen gratis oefenen.
0 van 5 vragen voltooid Vragen: Je hebt deze test al eerder afgerond, daarom kan je hem niet nog een keer doen.
Quiz is aan het laden… Je moet inloggen om deze quiz te starten. U moet eerst het volgende invullen:
0 van 5vragen goed beantwoord
Jouw tijd:
De tijd is verstreken
Je hebt 0 van 0 punten bereikt, 0
Earned Point(s): 0 of 0, (0)
Quiz samenvatting
Informatie
Resultaten
Resultaten
0 Audio(s)/Essay(s) Pending (Possible Point(s): 0)
Gemiddelde score
Your score
Categorieën
1. Vraag
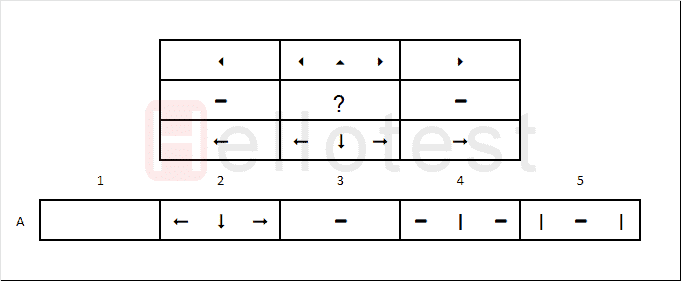
2. Vraag
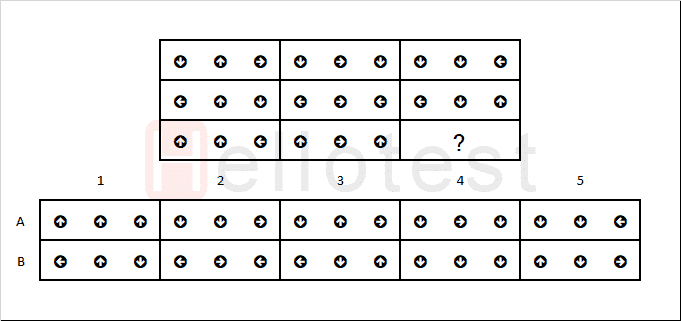
3. Vraag
4. Vraag
5. Vraag
Belangrijkste tip voor matrixen oefenen
Oefenen, oefenen, oefenen. Veel kandidaten vinden het matrix assessment het moeilijkste onderdeel wat je kan krijgen op een assessment. Zorg dus dat je niet alleen veel oefent maar ook specifiek. Want hoe gerichter je voorbereidt, hoe hoger jouw eindscore.
Inhoudsopgave
Wat meet matrix redeneren?
In het kort zijn matrixen een vorm om logisch redeneren tijdens een intelligentietest te toetsen. Het is een picturale test, waarbij afbeeldingen of matrix figuren worden gebruikt. Het figuur bij matrixen bestaat meestal 3 bij 3 vlakken. Dus 9 vlakken in totaal. Daarin zie je de abstracte informatie staan.
Het matrixen assessment staat bekend als cultuurvrij. Deels omdat bijvoorbeeld taal en opleiding geen rol spelen. Ook zijn de gebruikte vormen niet voorbehouden aan bijvoorbeeld West-Europa. Dus kan iedereen, ongeacht afkomst, opleiding of taal met elkaar vergeleken worden. Matrix redeneren is dus logisch of abstract redeneren waar iedereen op kan worden getest.
Matrixen uitleg
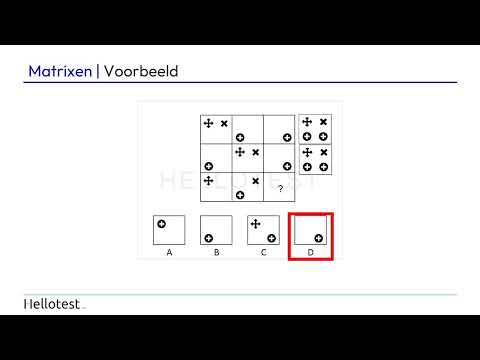
Voordat je een matrix kan oplossen, is het goed om te weten hoe een matrix er uitziet. Daarom leggen we hieronder uit hoe de abstracte matrix is opgebouwd.

De matrix bestaat (bijna) altijd uit 9 vlakken. Daarvan moet je dan het laatste vlak rechtsonder invullen. Bij sommige matrixen moet je het middelste of juist een ander deel invullen.
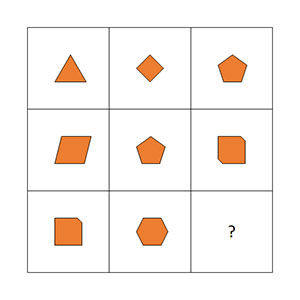
De vlakken worden gevuld met verschillende figuurtjes. Jij moet dan een relatie vinden tussen deze figuren. Het lastige aan matrixen is dat de relatie zowel horizontaal als verticaal kan zijn. Daarom moet je meerdere patronen proberen te ontwaren.
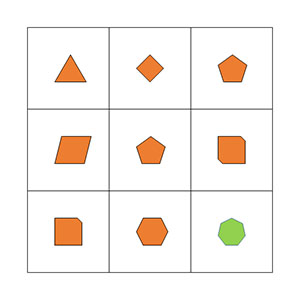
In het bovenstaande voorbeeld krijgen de figuren er telkens een hoek bij. Daarom moet het laatste figuur 7 hoeken hebben. De kleur wijkt af omdat we het antwoord duidelijk willen laten zien.
Matrixen voorbeelden
Hieronder zie je enkele voorbeelden van echte matrix vragen. Elk voorbeeld laat een andere verandering zien. Daardoor leer je alvast hoe matrixen kunnen verschillen.
Matrix redeneren voorbeeld 1
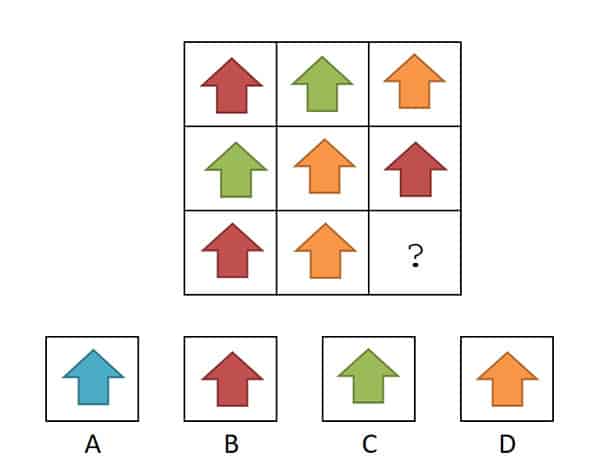
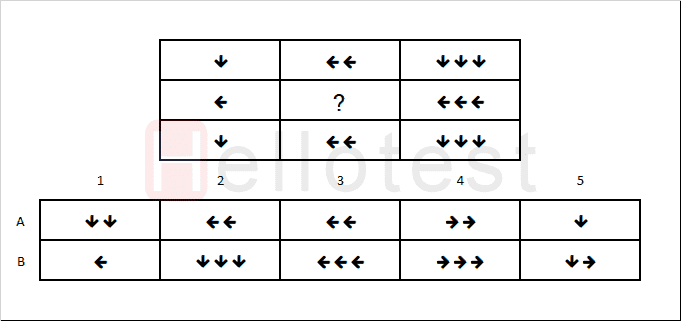
Deze matrix is relatief eenvoudig. Zie jij het antwoord al? Als je goed kijkt, zie je dat elke rij drie pijlen heeft van een andere kleur. Daarom moet in de laatste rij ook een groene pijl komen. Op zich is blauw ook een andere kleur, maar het is logischer dat er een groene pijl komt. De verticale verbanden zijn nu irrelevant.
Matrix redeneren voorbeeld 2
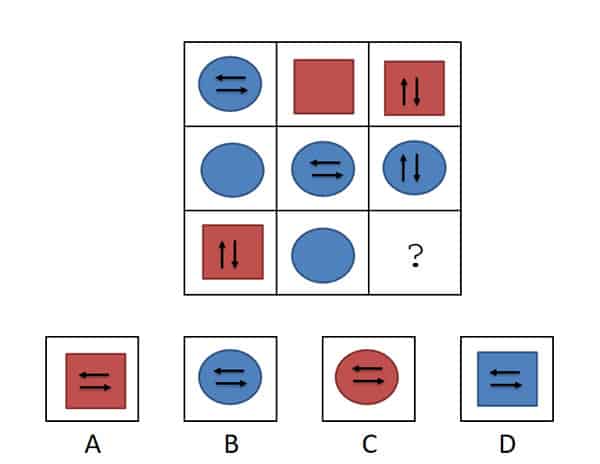
Nu zie je dat elke kolom twee blauwe cirkels heeft. Dus moet het antwoord een blauwe cirkels hebben en is het antwoord direct al B. Daarnaast zien we dat elke rij twee horizontale en twee verticale pijlen heeft. In de laatste rij moeten er nog horizontale pijlen bij. Dus ook dat bevestigt dat B het goede antwoord is.
Soorten abstracte matrixen
Er zijn veel verschillende soorten matrixen op het assessment. De matrix zelf is bedacht door John Raven in 1938. Daarom zul je vaak de naam Raven’s Progessive Matrices of Raven test tegenkomen. De precieze test die John Raven ontwikkelde, wordt niet meer gebruikt. Maar de testen zijn gebaseerd op zijn werk. De bekendste matrixen zie je hieronder.
LTP matrixen
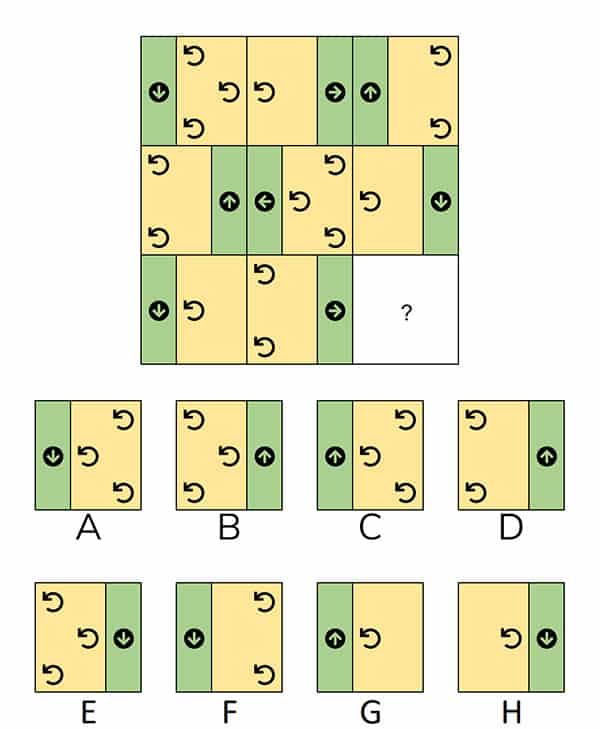
Dit soort matrixen kan je bij LTP verwachten. Wat je ziet is dat je veel meer antwoordopties hebt. Daardoor is gokken een stuk lastiger. Daarnaast is de inhoud ook anders. Zie jij het antwoord al? Hieronder leggen we het precies uit.
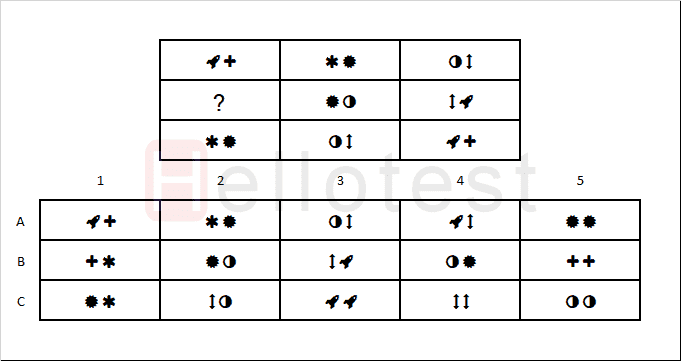
Elk vlak is verdeeld in een kleine en een grote rechthoek. Horizontaal gezien wordt het patroon L/R/R, R/L/R en L/R…/L gevolgd. De pijl in het zwarte rondje draait tegen de klok in. Verder heeft elke regel in totaal 6 rondjes met een pijl. Verdeeld volgens 3,1,2 2,3,1 en 1,2,…3 rondjes. Daarmee is het goede antwoord C.
PiCompany matrixen
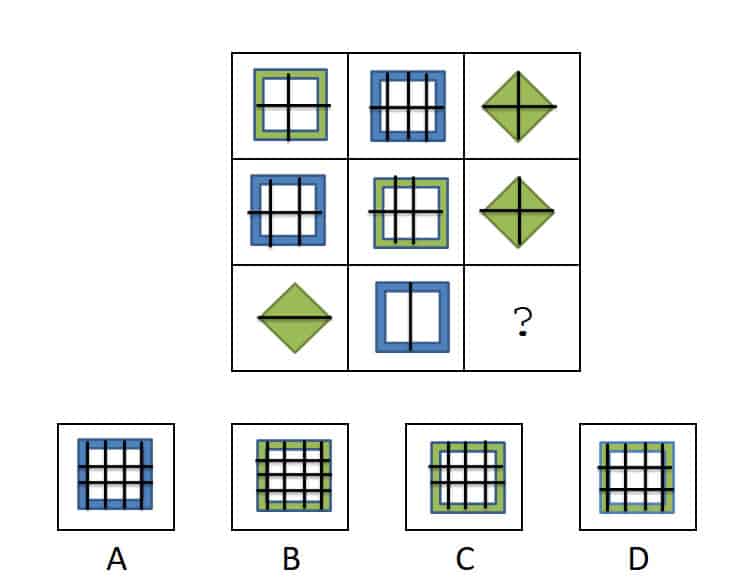
De PiCompany matrix is hetzelfde als onze eerdere voorbeelden. Zie jij het antwoord? Elke rij bevat 2 groene figuren. Daarnaast bevat elke rij bevat 3 horizontale strepen en 5 verticale. Dus antwoord D is het juiste antwoord.
Talent Q matrixen
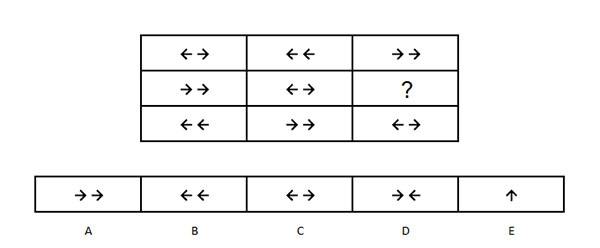
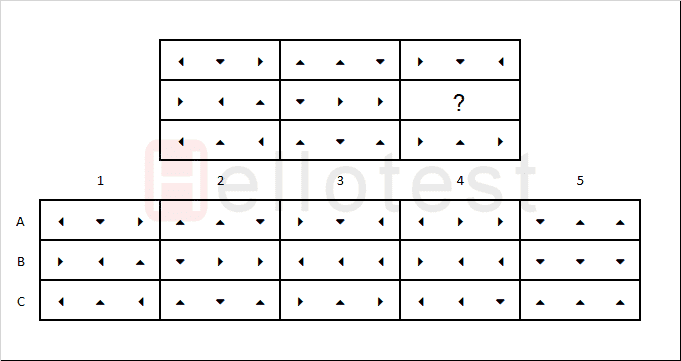
Dit is een eenvoudige Talent Q matrix. Zie jij het antwoord? Elke rij en kolom bevatten twee pijlen naar rechts, twee pijlen naar links en twee pijlen die uit elkaar staan. Daarmee is B het logische antwoord.
Verschil tussen figuurreeksen en matrixen
Het verschil tussen figuurreeksen en matrixen is vrij eenvoudig. Bij een figuurreeks staan de abstracte figuren in één rij, als volgt:
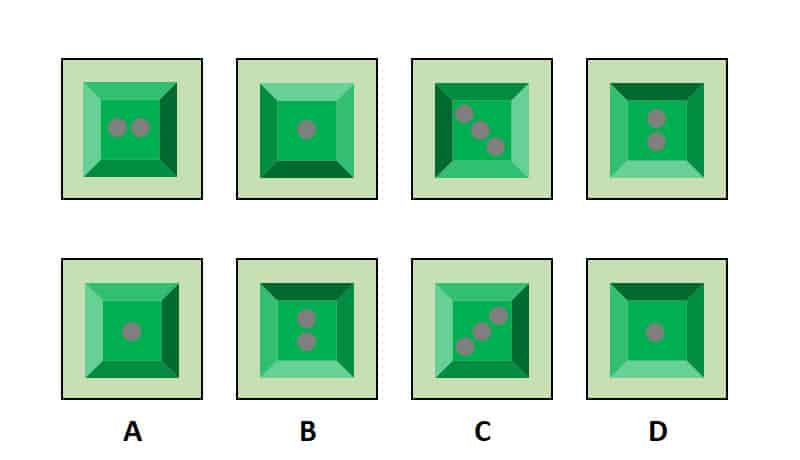
De bovenste rij is de figuurreeks en de tweede rij zijn de antwoorden.
Matrixen tips
- Zoek de verandering van de elementen. Kijk wat er gebeurt met de positie, kleur, vorm, grootte of het aantal.
- Verdeel de matrixen voor jezelf in rasters. Van bijvoorbeeld 3 bij 3. Dan zie je makkelijker hoe de elementen binnen de abstracte matrix bewegen.
- Leer patronen herkennen. Let op bewegingen als: horizontaal, verticaal, diagonaal, met de klok mee en tegen de klok in.
- Bekijk elk element apart. Ga niet alles tegelijk oplossen. Begin met 1 element. Sluit foute antwoorden uit en ga dan door naar het volgende element.
- Sluit foute antwoorden uit. Je hoeft niet het goede antwoord te bedenken! Je moet foute antwoorden uitsluiten tot er 1 antwoord over blijft. Als je dit doet los je misschien niet 4 maar slechts 2 elementen op. Dat scheelt heel veel tijd.
- De beste tip: oefen specifiek voor jouw assessment. Het is echt een wereld van verschil of je voor LTP, PiCompany of Talent Q moet oefenen.
By popular demand: free English translation included
This training offers practice materials in both English and Dutch, so you can choose your preferred language. The translations are included for free, a bonus we added in response to frequent customer requests.
Meer matrixen oefenen?
Wil jij meer oefenen voor het matrixen assessment? Kies dan voor ons oefenpakket. Voor slechts 14,99 kan jij 30 dagen lang oefenen voor de verschillende vormen van matrixen. Begin vandaag nog! Klik hier om ons oefenpakket aan jouw winkelwagen toe te voegen en af te rekenen.
Start direct met oefenen
Zorg voor een goede voorbereiding op jouw capaciteitentest.
Waarom Hellotest?
- Binnen 2 minuten starten
- 100% leeromgeving
- Mobiel, tablet en desktop
- Training op maat

Corstiaan Smit is oprichter van Hellotest en sinds 2013 actief als assessment trainer. Met zijn expertise in capaciteitentesten en strategieën heeft hij duizenden kandidaten succesvol voorbereid op hun assessment. Corstiaan is eindverantwoordelijk voor de ontwikkeling van al het oefenmateriaal en de trainingen, met als doel iedereen een eerlijke kans te geven op zijn of haar droombaan.
Veelgestelde vragen
In het kort zijn matrixen een bekende vorm om logisch redeneren tijdens een intelligentietest te toetsen. Het is een picturale test, waarbij afbeeldingen of matrix figuren worden gebruikt. Matrixen staan bekend als cultuurvrij. Deels omdat bijvoorbeeld taal en opleiding geen rol spelen. Ook zijn de gebruikte vormen niet voorbehouden aan bijvoorbeeld West-Europa. Dus kan iedereen, ongeacht afkomst, opleiding of taal met elkaar vergeleken worden. ‘Matrix redeneren’ is dus een soort van redeneren waar iedereen op kan worden getest.
De matrix is bedacht door John Raven in 1938 en wordt daarom ook wel Raven’s Progressive Matrices, of simpelweg ‘Raven test’, genoemd. John Raven ontwikkelde drie variaties op de Raven progressive matrices test:
- Standard Progressive Matrices
- Advanced Progressive Matrices
- Coloured Progressive Matrices
Deze drie Raven testen worden eigenlijk niet meer gebruikt. Wel wordt de vorm zoals die door John Raven bedacht is, gebruikt.
Bij een matrix verandert er telkens iets volgens een bepaalde regel. Een aantal eenvoudige verbanden zijn:
- Vermeerderen: er komt telkens een figuur / hoek bij.
- Verminderen: er gaat telkens een figuur / hoek af.
- Draaien: een figuur draait met de klok mee / tegen de klok in.
- Uiterlijk: de kleur, vorm, vulling en grootte, rand veranderen.
Los het verband daarna op:
- Ga op zoek naar het verband. Er kunnen natuurlijk ook meerdere verbanden zijn.
- Kijk naar de antwoordmogelijkheden en selecteer de mogelijkheden met het juiste verband.
- Als het antwoord er niet tussen lijkt te staan, streep dan antwoorden weg die in ieder geval niet het verband hebben.
Bij een aantal bureaus kom je nog de Raven test tegen, zoals bij Pearson. Daarnaast hebben LTP, PiCompany en Talent Q hun eigen matrix test ontwikkeld.
In het kort zijn matrixen een bekende vorm om logisch redeneren tijdens een intelligentietest te toetsen. Het is een picturale test, waarbij afbeeldingen of matrix figuren worden gebruikt. Matrixen staan bekend als cultuurvrij. Deels omdat bijvoorbeeld taal en opleiding geen rol spelen. Ook zijn de gebruikte vormen niet voorbehouden aan bijvoorbeeld West-Europa. Dus kan iedereen, ongeacht afkomst, opleiding of taal met elkaar vergeleken worden. ‘Matrix redeneren’ is dus een soort van redeneren waar iedereen op kan worden getest.
De matrix is bedacht door John Raven in 1938 en wordt daarom ook wel Raven’s Progressive Matrices, of simpelweg ‘Raven test’, genoemd. John Raven ontwikkelde drie variaties op de Raven progressive matrices test:
- Standard Progressive Matrices
- Advanced Progressive Matrices
- Coloured Progressive Matrices
Deze drie Raven testen worden eigenlijk niet meer gebruikt. Wel wordt de vorm zoals die door John Raven bedacht is, gebruikt.
Het meervoud van matrix is matrices of matrixen.
Bij een matrix verandert er telkens iets volgens een bepaalde regel. Een aantal eenvoudige verbanden zijn:
- Vermeerderen: er komt telkens een figuur / hoek bij.
- Verminderen: er gaat telkens een figuur / hoek af.
- Draaien: een figuur draait met de klok mee / tegen de klok in.
- Uiterlijk: de kleur, vorm, vulling en grootte, rand veranderen.
Los het verband daarna op:
- Ga op zoek naar het verband. Er kunnen natuurlijk ook meerdere verbanden zijn.
- Kijk naar de antwoordmogelijkheden en selecteer de mogelijkheden met het juiste verband.
- Als het antwoord er niet tussen lijkt te staan, streep dan antwoorden weg die in ieder geval niet het verband hebben.
In het kort zijn matrixen een bekende vorm om logisch redeneren tijdens een intelligentietest te toetsen. Het is een picturale test, waarbij afbeeldingen of matrix figuren worden gebruikt. Matrixen staan bekend als cultuurvrij. Deels omdat bijvoorbeeld taal en opleiding geen rol spelen. Ook zijn de gebruikte vormen niet voorbehouden aan bijvoorbeeld West-Europa. Dus kan iedereen, ongeacht afkomst, opleiding of taal met elkaar vergeleken worden. ‘Matrix redeneren’ is dus een soort van redeneren waar iedereen op kan worden getest.
De matrix is bedacht door John Raven in 1938 en wordt daarom ook wel Raven’s Progressive Matrices, of simpelweg ‘Raven test’, genoemd. John Raven ontwikkelde drie variaties op de Raven progressive matrices test:
- Standard Progressive Matrices
- Advanced Progressive Matrices
- Coloured Progressive Matrices
Deze drie Raven testen worden eigenlijk niet meer gebruikt. Wel wordt de vorm zoals die door John Raven bedacht is, gebruikt.
Laatst geüpdatet op:


